Diagrama de temas
General
Presentación
Qué es una sección cónica?
En geometría analítica, las secciones cónicas (o simplemente cónicas) son todas las curvas resultantes de las diferentes intersecciones entre un cono recto doble y un plano, cuando ese plano no pasa por el vértice del cono. Existen cuatro tipos de secciones cónicas: la circunferencia, la elipse, la parábola y la hipérbola, dependiendo de la inclinación que tenga el plano.
A continuación, se muestra la representación gráfica de las cuatro cónicas resultantes:
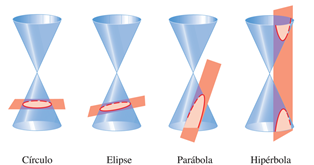
En lo que resta del curso se detallarán las características y propiedades de cada una.
LA CIRCUNFERENCIA
ORIGEN
La circunferencia es formada a partir de la intersección de un cono recto doble con un plano inclinado, el cuál es paralelo a la base del cono, como se muestra en la figura:
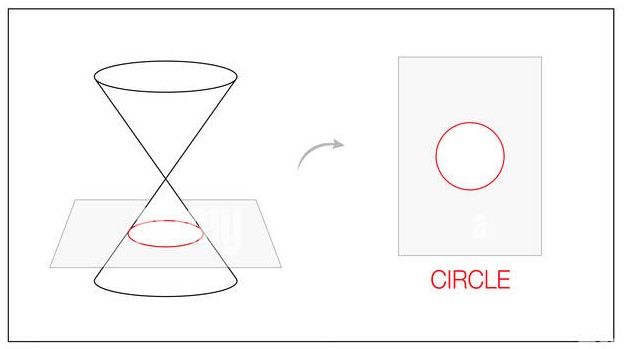
DEFINICIÓN
Se define como el lugar geométrico de todos los puntos del plano que equidistan de un punto fijo llamado centro.
\( Circunferencia= \lbrace{P(x,y)|d(C,P)=r, r>0 }\rbrace \) con Centro: C(x0 , y0)
Teniendo en cuenta la siguiente imagen podemos construir la expresión algebraica que representa a la circunferencia.
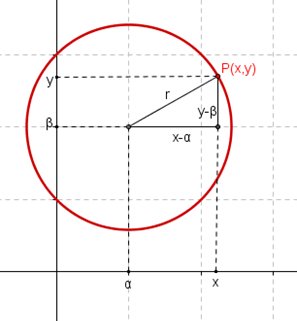
Por teorema de Pitágoras sabemos que los puntos deben cumplir con lo siguiente:
\( (x- \alpha)^2+(y- \beta)^2=r^2 \)
Que corresponde a la ecuación principal de una circunferencia con centro en \( C(\alpha, \beta) \) y radio r. Si el centro fuera el punto (0,0), entonces la ecuación quedaría:
\( (x- 0)^2+(y- 0)^2=r^2 \Rightarrow x^2+y^2=r^2 \)
La cual se denomina como ecuación canónica de una circunferencia.
Ahora, si desarrollamos los cuadrados de binomio de la ecuación principal nos queda lo siguiente:
\( (x- \alpha)^2+(y- \beta)^2=r^2 \Rightarrow x^2+2 \alpha x+ \alpha^2+y^2-2 \beta y+ \beta^2=r^2 \)
\( x^2+y^2-2 \alpha x-2 \beta y+( \alpha^2+ \beta^2+r^2)=0 \)
Luego, renombramos las constantes y nos queda:
\( x^2+y^2+Dx+Ey+F=0 \)
que es la ecuación general de una circunferencia.
Si hacemos este ejercicio a la inversa, es decir, pasar de una ecuación general a una ecuación principal debemos completar cuadrados de binomio para obtener todos los términos algebraicos que lo forman al desarrollarlo.
Hay que tener en cuenta que:
- Si \( r^2>0 \rightarrow \) es circunferencia.
- Si \( r^2=0 \rightarrow \) es un punto.
- Si \( r^2<0 \rightarrow \) conjunto vacío.
En este espacio usted podrá presentar todas sus dudas con respecto a este capítulo y serán respondidas a la brevedad.
En el siguiente archivo encontrarás una guía para que practiques y refuerces los contenidos aprendidos con respecto a este tema.
LA ELIPSE
ORIGEN
Corresponde a la intersección de un cono recto doble con un plano inclinado, el cual atraviesa oblicuamente uno de los conos, como se muestra en la imagen:
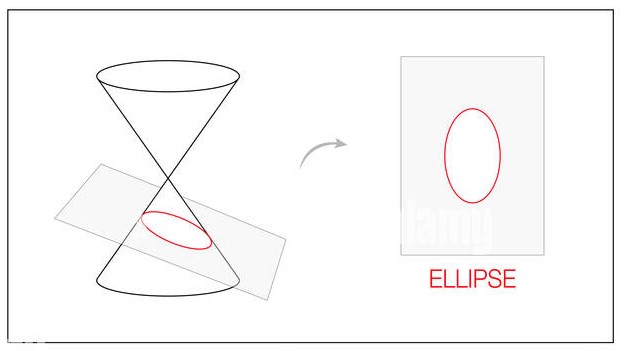
DEFINICIÓN
Se define como el lugar geométrico de todos los puntos del plano que, dado dos puntos fijos, la suma de las distancias a estos puntos es constante. Esto es:
\( \epsilon= \lbrace{P(x,y)|d(P,F_1)+d(P,F_2)=cte }\rbrace \)
A continuación, se observa una elipse cualquiera, con focos A y B, y un punto D que muestra el lugar que toman todos los puntos que componen a la cónica. Utilizando la función de suma se demuestra que, independiente de la posición del punto D, la suma de las distancias a los focos (a) siempre es constante.
ELEMENTOS
La ecuación que representa a una elipse con centro (0,0), focos F1(-c,0), F2(c,0) y eje focal y=0 (eje x) es la siguiente:
\( \frac{x^2}{a^2}+ \frac{y^2}{b^2}=1 \)
Si buscamos las intersecciones de la elipse con los ejes, observamos que:
\( y=0: x^2=a^2 \Rightarrow x= \pm a \Rightarrow V_1(a,0); V_2(-a,0) \)
\( x=0: y^2=b^2 \Rightarrow y= \pm b \Rightarrow V_3(-b,0); V_4(b,0) \)
Estos cuatro puntos se denominan vértices de la elipse.
Luego, tenemos que:
- a se denomina al semieje mayor.
- b se denomina al semieje menor.
- c es la semidistancia focal: distancia del centro a uno de los focos.
- 2c es la distancia entre ambos focos.
- Eje focal es la recta que pasa por ambos focos.
A continuación, se muestra la gráfica de todos estos elementos:
Observen que el origen es el centro de simetría de la elipse.
Si en la ecuación anterior permutamos x por y, queda:
\( \frac{y^2}{a^2}+ \frac{x^2}{b^2}=1 , a>b \)
En este caso las coordenadas de los vértices y focos son:
- Vértices: \( V_1(0,a); V_2(0,-a); V_3(-b,0); V_4(b,0) \)
- Focos: \( F_1(0,-c); F_2(0,c) \)
Y su gráfica es:
Excentricidad
Es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia que comparte el mismo centro. Se calcula mediante la razón:
\( e= \frac{c}{a} \)
En la siguiente imagen podrás ver cómo va cambiando la excentricidad de la elipse a medida que aumentamos o disminuimos el valor de a, moviendo el punto P, y cómo esto influye en la forma que toma la figura.
LA PARÁBOLA
ORIGEN
Se forma a partir de la intersección de un cono recto con un plano inclinado, el cual corta oblicuamente la base del cono, como se muestra en la siguiente imagen:
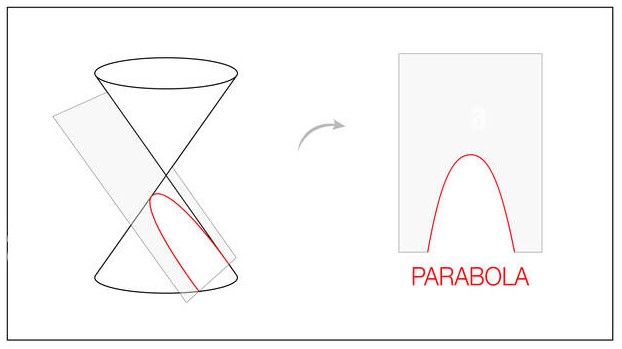
DEFINICIÓN
Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo F (foco) y una recta r llamada Directriz. Esto es:
\( Parábola: P_a= \lbrace{P(x,y)|d(P,r)=d(P,F) }\rbrace \)
En definitiva, es un conjunto de puntos que verifican cierta propiedad geométrica, pero que no se limita a ser la gráfica de una función cuadrática.
A continuación, se muestra una representación gráfica de la cónica, donde podemos ver que, independiente de la posición del punto P, la distancia de éste a la directriz y al foco F es la misma.
Podemos observar en la imagen que la recta y=0 es eje focal o eje de simetría de la parábola, y que el punto (0,0) es su vértice, punto en el que cambia la dirección de la cónica.
ELEMENTOS
La ecuación que representa una parábola con vértice V(0,0), foco F(c,0) y directriz: x=-c es la siguiente:
\( y^2=4cx \)
Llamada ecuación canónica de la parábola. Donde se cumple que:
- Si \( c>0 \Rightarrow \) Las ramas de la parábola apuntan hacia la derecha.
- Si \( c<0 \Rightarrow \) Las ramas de la parábola apuntan hacia la izquierda.
Estas dos situaciones están representadas por la siguiente gráfica:
Luego, si permutamos variables sobre la expresión canónica de una parábola con eje focal horizontal podemos encontrar la expresión canónica para la parábola con eje focal vertical, que queda de la siguiente forma:
\( x^2=4yc \)
Donde el vértice será V(0,0), el eje focal x=0, el foco F(0,c) y la direcriz: y=-c, y se cumplirá que:
- Si \( c>0 \Rightarrow \) Las ramas de la parábola apuntan hacia arriba.
- Si \( c<0 \Rightarrow \) Las ramas de la parábola apuntan hacia abajo.
Estas dos situaciones están representadas por la siguiente gráfica:
Ahora, si trasladamos en el plano las parábolas correspondientes a cada una de las ecuaciones canónicas, obtendremos las siguientes ecuaciones principales:
- \( (y- \beta)^2=4c(x- \alpha) \), la cual tendrá como vértice \( V( \alpha, \beta) \) y un eje focal paralelo al eje x.
- \( (x- \alpha)^2=4c(y- \beta) \), la cual tendrá como vértice \( V( \alpha, \beta) \) Y un eje focal paralelo al eje y.
Luego, si desarrollamos los cuadrados de binomio tenemos:
- Para 1:
\( y^2-4cx-2 \beta y+ \beta^2+4c \alpha=0 \)
Renombramos los coeficientes y nos queda:
\( y^2+Dx+Ey+F=0 \)
La cual se conoce como ecuación general de la parábola con eje horizontal.
- Para 2:
\( x^2-4cy-2 \alpha x+ \alpha^2+4c \beta =0 \)
Renombramos los coeficientes y nos queda:
\( x^2+Dy+Ex+F=0 \)
La cual se conoce como ecuación general de la parábola con eje vertical.
LADO RECTO
El lado recto es la longitud de la cuerda que es perpendicular al eje focal y pasa por el foco. Se puede demostrar que la longitud del lado recto es \( |4c| \). A continuación se observa la gráfica de este elemento, donde además podemos modificar la distancia c, entre el vértice y el foco, lo que afectará directamente a la longitud del lado recto.
LA HIPÉRBOLA
ORIGEN
Corresponde a la intersección de un cono recto doble con un plano el cual es perpendicular a las bases del cono, como se muestra en la siguiente figura:
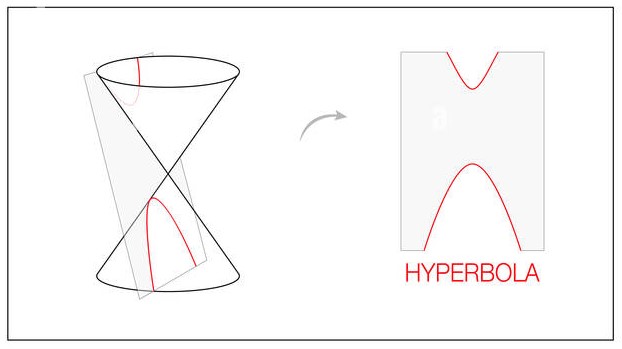
DEFINICIÓN
Es el lugar geométrico de todos los puntos del plano que, dado dos puntos fijos F1 y F2 (focos), el valor absoluto de la diferencia de sus distancias a los focos es constante.
\( H= \lbrace{P(x,y)| |d(P;F_1)-d(P;F_2)|=2a=cte }\rbrace \)
A continuación, se muestra la representación gráfica de esta cónica, donde se puede observar que el valor absoluto de la diferencia de distancias es constante.
Esto está condicionado por la siguiente restricción:
Si la distancia entre los focos es \( d(F_1,F_2)=2c \) \( \Rightarrow c>a>0 \)
\( \Rightarrow c^2>a^2 \)
\( \Rightarrow c^2-a^2=b^2 \)
\( \Rightarrow c^2=a^2+b^2 \)
ELEMENTOS
La ecuación que representa una hipérbola con centro en (0,0) y eje focal y=0 (eje x) es la siguiente:
\( \frac{x^2}{a^2}- \frac{y^2}{b^2}=1 \)
La cual se denomina ecuación canónica de la hipérbola con centro (0,0) y eje focal y=0, y se deduce de la gráfica de forma similar que en la Elipse. Y su representación gráfica es la siguiente:
Ahora, si buscamos las intersecciones de la cónica con los ejes cartesianos obtenemos lo siguiente:
\( y=0 \Rightarrow \left| x \right| =a \Rightarrow x= \pm a \Rightarrow V_1=(a,0); V_2=(-a,0) \)
\( x=0 \Rightarrow y^2=-b^2 \)
Donde V1 y V2 son vértices de la hipérbola y ésta no corta al eje y. Además, sabemos que \( F_1(-c,0) \) y \( F_2(c,0) \) son focos. Por otro lado, a se denomina semieje real o transverso, b se denomina semieje imaginario y 2c es la distancia entre los focos. Aparece también un nuevo elemento que no existe en las demás cónicas, las asíntotas, las cuales tendrán como ecuación de la recta: \( y= \pm \frac{b}{a}x \).
Si en la ecuación canónica anterior permutamos x por y queda:
\( \frac{y^2}{a^2}- \frac{x^2}{b^2}=1 \)
Que es la ecuación canónica de una hipérbola con centro en (0,0) y eje focal x=0 (eje y). Su representación gráfica es la siguiente:
Ahora, si buscamos las intersecciones de la cónica con los ejes cartesianos obtenemos lo siguiente:
\( x=0 \Rightarrow \left| y\right|=a \Rightarrow y= \pm a \Rightarrow V_1=(0,a); V_2=(0,-a) \)
\( y=0 \Rightarrow x^2=-b^2 \)
Donde V1 y V2 son vértices de la hipérbola y ésta no corta al eje x. Además, sabemos que \( F_1(0,c) \) y \( F_2(0,-c) \) son focos. Por otro lado, a se denomina semieje real o transverso, b se denomina semieje imaginario y 2c es la distancia entre los focos. Aparece también un nuevo elemento que no existe en las demás cónicas, las asíntotas, las cuales tendrán como ecuación de la recta: \( y= \pm \frac{a}{b}x \).
Para determinar si el eje focal es horizontal o vertical solo basta observar los coeficientes de cada variable:
- Si el coeficiente de x2 es positivo, sabemos que el eje focal es el eje x.
- Si el coeficiente de y2 es positivo, sabemos que el eje focal es el eje y.
Para una hipérbola con centro en cualquier punto del plano cartesiano tenemos:
- La ecuación principal de una hipérbola con eje focal horizontal y centro en es:
\( \frac{(x- \alpha) ^2 }{a^2}- \frac{(y- \beta)^2}{b^2} =1 \)- La ecuación principal de una hipérbola con eje focal vertical y centro en es:
\( \frac{(y- \beta)^2}{a^2}- \frac{(x- \alpha)^2}{b^2}=1 \)
RESUMEN
- En este link encontrarás un resumen con las principales características y elementos de cada cónica, desarrollado en un cuadro de síntesis.
- En los siguientes links encontrarás ejercicios resueltos sobre cónicas para que puedas practicar.
https://ocw.unizar.es/ocw/pluginfile.php/72/mod_label/intro/u5conreto.pdf
https://matematicasiesoja.files.wordpress.com/2013/10/conicas.pdf
https://matematicasies.com/spip.php?page=resueltos2&tema=118
APLICACIONES DE LAS CÓNICAS
A continuación, te he dejado unos videos en los cuales se muestran algunas de las aplicaciones que se le han hecho a las cónicas en diferentes ámbitos de la vida cotidiana. Te invito a verlos.
Video 1
Video 2
Video 3
