Diagrama de temas
Presentación del curso




¿Qué es una homotecia?
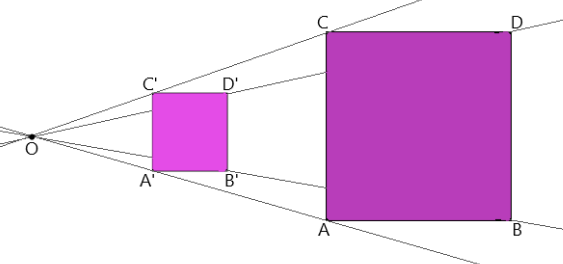
Cuando hablamos de Homotecia nos referimos a la transformación geométrica con la cual se obtiene una figura a partir de ampliar, reducir o mantener el tamaño de otra. Esto es posible estableciendo una razón (k) entre la distancia de un punto fijo llamado centro (O) y los vértices de las figuras.
A la figura que obtenemos al aplicar una homotecia le llamamos figura resultante o imagen y denotamos sus vértices con las mismas letras de la figura original. Para no confundir los nombres de los vértices, le ponemos apóstrofes (') a los de la figura imagen, de esta manera si nuestra figura original es el triángulo ABC, la figura resultante será el triángulo A'B'C'.
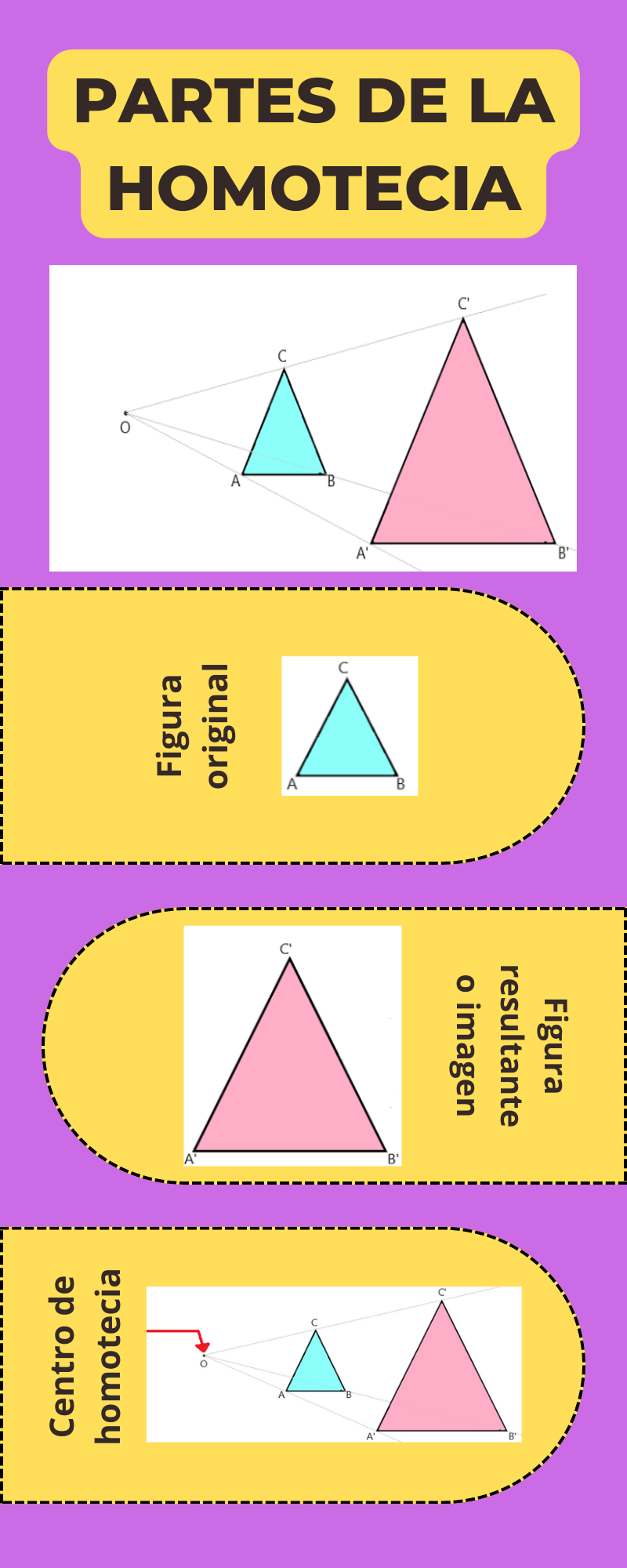
Al realizar una homotecia, la figura original y la figura imagen son semejantes, esto quiere decir que sus ángulos son congruentes y sus lados homólogos son proporcionales. Esto último tiene relación con la razón de homotecia, sigue leyendo!
Razón de homotecia
La razón de homotecia (k) corresponde al cociente entre la distancia desde O hasta cada vértice de la figura original y a la distancia desde O hasta cada vértice de la figura resultante.
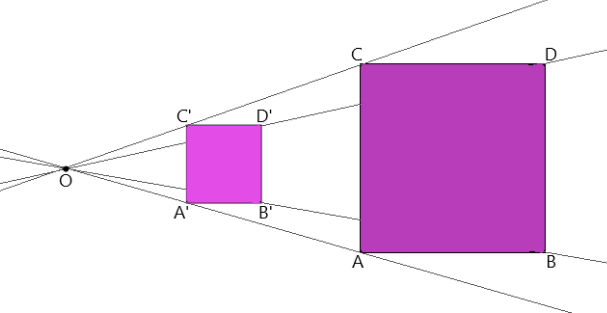
Por ejemplo, en la homotecia presentada en la imagen, la razón de homotecia es:
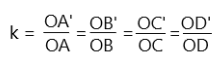
Tipos de homotecia
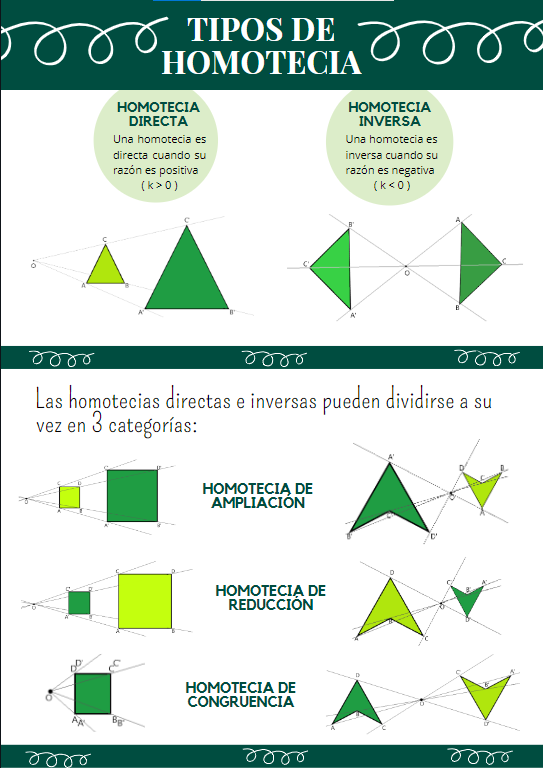
+ información sobre homotecias
Antes de continuar con el curso, te invito a ver este video a modo de resumen de lo aprendido sobre homotecia.
Si aún tienes dudas no te preocupes, quizás necesitas que te lo expliquen desde otra perspectiva. Puedes encontrar más información sobre los temas tratados en el curso en las siguientes páginas web:
Antes de continuar...
La personita que aparece acá abajo es Sam, ayúdale a estudiar respondiendo a sus preguntas. Presiona la bandera verde para comenzar.Teorema particular de Tales
El teorema de Tales es una ley de la geometría que nos indica que si se traza un segmento paralelo a cualquiera de los lados de un triángulo tendremos como resultado un triángulo semejante el triángulo original.Que dos triángulos sean semejantes quiere decir que:
-Sus ángulos correspondientes miden lo mismo.
-La razón entre los lados correspondientes es la misma para los 3 lados.
Veamos el Teorema de Tales con el siguiente ejemplo:
Tenemos un triángulo ABC al cual se le traza una segmento PQ paralelo a AB.
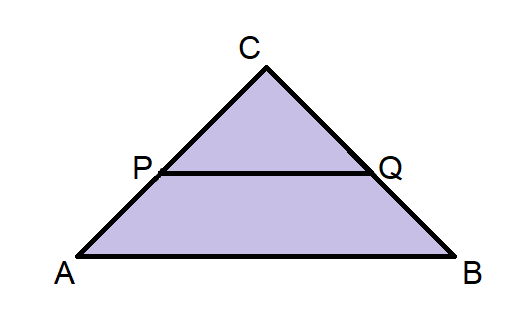
Notemos que si PQ es paralelo a AB, se va a cumplir el Teorema de Thales, es decir, ΔABC semejante a ΔPQC.
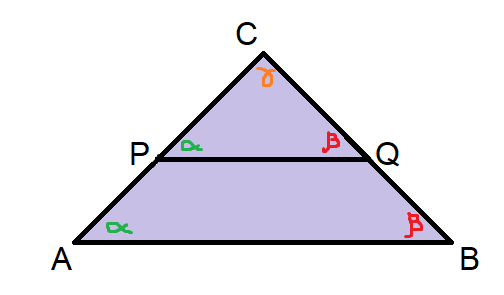
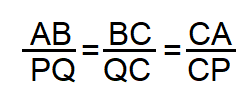
A continuación haz click en "Ejercicio". Te aparecerán los triángulos ΔABC y ΔPQC en el cual el segmento PQ es paralelo a AB. Mueve los vértices A, B o C y fíjate en lo que ocurre con los distintos ángulos. Si notas algo puedes dejar un comentario en la sección "Observaciones".
Extensión del Teorema de Tales
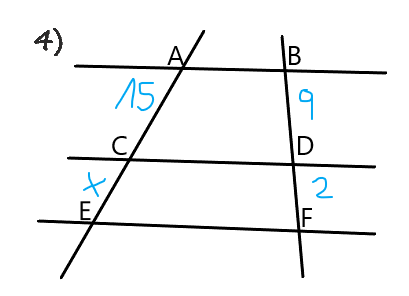
El teorema particular de Tales puede extenderse a dos rectas cualquiera que son cortadas por rectas paralelas entre sí, formando las siguientes razones:
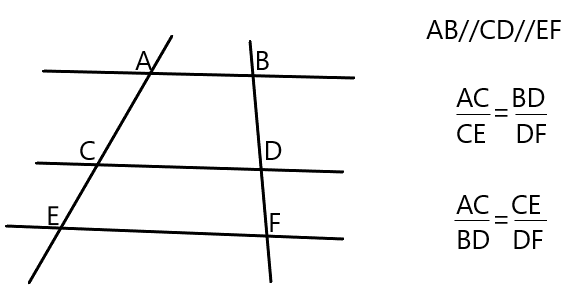
Conociendo estas razones puedes encontrar el valor de x en los siguientes ejercicios:
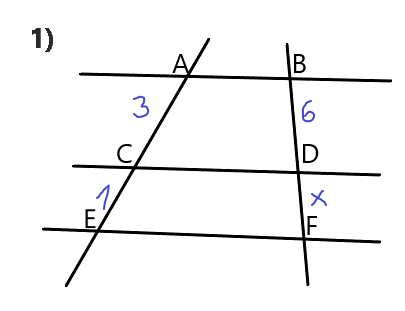
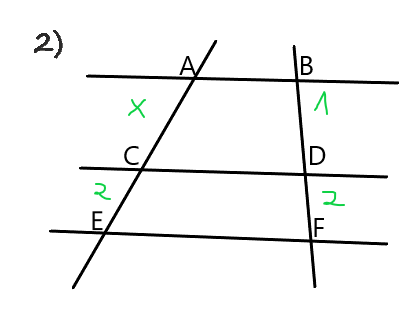
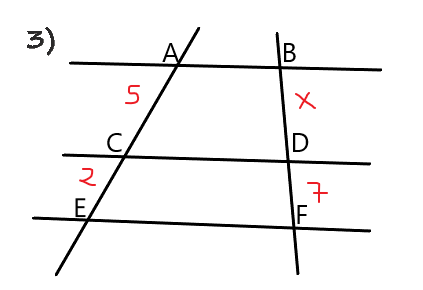
El programa de acá abajo te sirve para comprobar que la razón entre los lados a, b, c y d es correcta. Puedes darles valor numérico a estas fracciones haciendo click en las letras naranjas. Presiona la barra espaciadora cuando ya hayas escrito los 4 valores para saber si la razón es correcta o no.
*Los números decimales escríbelos con punto (por ejemplo: 17.5)+ información sobre teorema de Tales
Antes de continuar con el curso, te invito a ver este video a modo de resumen de lo aprendido sobre teorema de Tales.
Si aún tienes dudas no te preocupes, quizás necesitas que te lo expliquen desde otra perspectiva. Puedes encontrar más información sobre los temas tratados en el curso en las siguientes páginas web:Aplicación de lo aprendido




Test final
