Diagrama de temas

  • ¿Qué son las transformaciones isométricas?

    Para dar respuesta a la pregunta de introducción, debemos recurrir a la etimología y significados de las palabras clave. En primer lugar, ¿Qué es transformación? La palabra "transformación" proviene del latín transformatio y sus componentes léxicos son: el prefijo trans- (de un lado a otro), forma (figura, imagen), más el sifijo -ción (acción y efecto); lo que significa en conjunto "acción y efecto de cambiar de una forma a otra". En segundo lugar, nos preguntamos ¿Qué es isométrico? La palabra es proviene de orignes griegos y sus componentes léxicos son: iso (igual), metron (medida), más el sufijo -ico (relativo); lo que interpretamos como dimensiones iguales.

    Entonces, basados en la etimología, podemos entender a las transformaciones isométricas como la acción de cambio con respecto a la posición de una figura en donde se conservan sus formas y tamaños.

    A continuación, véase un efecto maravilloso generado por las transformaciones isométricas, el cual conocemos por eclipse en donde interactúa la luna, el sol y nuestra perspectiva desde la tierra.


    • Siguiendo el Currículum Matemático Chileno tenemos el siguiente objetivo:
      Curso 8°Básico.
      Unidad 3: Teorema de Pitágoras. Prismas y cilindros. Posición y movimientos.

      Objetivo MAo8 OA14: Componer rotaciones, traslaciones y reflexiones en el plano cartesiano y en el espacio, de manera manual y/o con software educativo, y aplicar a las simetrías de polígonos y poliedros, y a la resolución de problemas geométricos relacionados con el arte.


    • Objetivo especifico: Entender las transformaciones isométricas a través de ejemplos y construcciones realizadas con ayuda de GeoGebra.

  • Introducción



    • Conocimientos previos

      Algunas definiciones relacionadas a las construcciones geométricas:

      • Plano: Es la superficie y/o espacio donde se pueden trazar rectas y puntos. Usaremos un plano de dos dimensiones, longitud y anchura.
      • Punto: Es el objeto más pequeño del espacio, no tiene dimensión, es decir, ni longitud ni anchura.
      • Recta: Dados dos puntos es una única línea que los une y, se proyecta teniendo una dimensión de longitud infinita. (No posee anchura).
      • Semirrecta: Es una recta, pero tiene un punto de partida.
      • Segmento: Es una parte de cierta recta, limitada por dos puntos. No tiene anchura, pero si cierta longitud.
      • Vector: Segmento de recta en el espacio que parte de un punto hacia otro, es decir, que tiene dirección, magnitud y sentido. Se representa por una flecha en el plano.
      • Ángulos: Es una parte del plano comprendida por dos semirrectas.
      • Perpendicular: Un par de rectas son perpendiculares, si al intersecarse forman un ángulo de 90°. También, pueden ser segmentos.
      • Circunferencia: Es una cónica que consta de un centro y un radio, donde todos los puntos que la conforman están a la misma longitud al centro, dicha longitud es el radio.
      • Figura: Forma exterior de un cuerpo.

    • Rotación respecto a un vértice

      Una rotación con respecto a un vértice es una transformación isométrica que consiste en que una figura cualquiera sea, cambia su sentido u orientación positiva o negativamente, dado un ángulo y manteniendo uno de sus vértices como punto de "rotación".

      Por ejemplo, podríamos considerar a una bailarina de ballet.


      • ¿Cómo construir una rotación respecto a un vértice de la figura en GeoGebra?

        Enlace GeoGebra: https://www.geogebra.org/classic#geometry

      • Animación de una Rotación respecto a un vértice con GeoGebra:


      • Para reflexionar:

        1. ¿Qué ocurre cuando el ángulo tiene 0°?
        2. ¿Qué sucede cuando el ángulo es de 360°?
        3. ¿Qué pasa cuando el ángulo mide 180°?
        4. ¿Qué pasaría si los ángulos fueran negativos?


    • Rotación respecto a un punto arbitrario

      La siguiente transformación isométrica que veremos, es otra rotación dado un ángulo, pero ahora con respecto a un punto cualquiera en el espacio, es decir, existe un cambio de orientación o sentido positiva o negativamente de una figura cualquiera sea con respecto a un punto arbitrario. Cabe mencionar, que las rotaciones de 360° cumplen un ciclo y la figura queda en su posición inicial, esto se debe, a que la rotación se elabora únicamente en base a la circunferencia.

      Por ejemplo, podríamos considerar un carrusel.


      • ¿Cómo construir una rotación respecto a un punto en el plano con GeoGebra?

        Enlace Geogebra: https://www.geogebra.org/classic#geometry


      • Animación de una rotación respecto a un punto en el plano con GeoGebra:


      • Para reflexionar:

        1. ¿Qué ocurre con la figura en los ángulos de 0° y 360°?
        2. ¿Qué sucede si movemos la figura inicial?
        3. ¿Qué pasa si movemos el punto centro de rotación?
        4. ¿Qué pasaría si ubicamos el punto centro de rotación en el centro de la figura?

    • Traslación

      Otro tipo de transformación isométrica son las traslaciones, aquella indica mover una figura u objeto dado un vector, lo que permite reubicar el objeto a disposición nuestra sin cambiar sus características originales. Con respecto al vector, es aplicado a cada uno de los vértices de la figura u objeto, logrando un movimiento de cierta magnitud y sentido.

      Por ejemplo, pensemos en el andar de un caracol (cualquier animal) e, incluso en medios de transporte, etc.

      • ¿Cómo construir una traslación de una figura con GeoGebra?

        Enlace GeoGebra: https://www.geogebra.org/classic#geometry


      • Animación de una Traslación con GeoGebra.


      • Para reflexionar:

        1. Sabiendo que el deslizador "a" representa los valores del eje "x" ¿Qué pasa si movemos este deslizador? 
        2. Sabiendo que el deslizador "b" representa los valores del eje "y" ¿Qué pasa si movemos este deslizador? 
        3. ¿Cuál es la función del vector? ¿En qué afecta su dirección y magnitud?

    • Simetría Central

      La simetría es la transformación que nos permite, como dice la palabra, reflejar una figura por medio de un punto focal o de una recta focal. Esta figura al ser reflejada no cambia su forma, pero si, su dirección. Es lo que se llama efecto espejo. Existen dos tipos de simetría: Axial y central. 

      La simetría central es el reflejo respecto a un punto llamado foco, además los puntos de la figura y el foco crean rectas en donde a una misma distancia se encuentra el punto reflejado de la nueva figura. Este tipo de transformación isométrica invierte la figura.

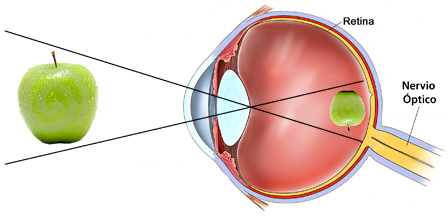
      Por ejemplo, nuestros ojos perciben el mundo en función de una simetría central y es nuestro cerebro quien orienta nuevamente la imagen.


      • ¿Cómo construir una simetría central de una figura con GeoGebra?

        Enlace GeoGebra: https://www.geogebra.org/classic#geometry


      • Animación de Simetría Central con GeoGebra:


      • Para reflexionar:
        1. ¿Qué sucede si se mueve el punto central o focal? 
        2. ¿Qué ocurre si se mueve el polígono completo? 
        3. ¿Qué pasa si se mueve el punto A? ¿O el B? ¿O el C?

    • Simetría Axial

      La simetría axial se puede entender como un reflejo respecto a un Eje de simetría, donde todos los puntos de la figura coinciden con los de la figura reflejada al otro lado del eje y, son equidistantes al eje de simetría. 

      Por ejemplo, la naturaleza nos ofrece instantes en donde los lagos realizan una simetría axial del paisaje.


      • ¿Cómo construir una Simetría Axial en GeoGebra?

        Enlace GeoGebra: https://www.geogebra.org/classic#geometry


      • Animación de simetría axial en Geogebra:


      • Para reflexionar:
        1. ¿Qué pasa si se mueve el punto A? ¿Y si se mueve el punto B?
        2. ¿Al mover solo un punto se mueve la figura completa? Explicar
        3. ¿Qué sucede si mueve el eje de reflexión?
        4. ¿Qué ocurre si el punto C, se encuentra al otro lado del eje?

    • Para finalizar