Topic outline
General
Álgebra
(Para 1º y 2º medio)
El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades. Es una de las principales ramas de la matemática, junto a la geometría, el análisis matemático, la combinatoria y la teoría de números.
El álgebra, tiene como objetivo fundamental el analizar de manera muy simple y en forma alfanumérica las actividades u operaciones diarias; donde los elementos, actividades o elementos que intervienen en un proceso, son reemplazados en una ecuación donde son representados por símbolos numéricos o alfanuméricos.
Contenidos del curso
1.- Historia del álgebra
2.- Álgebra para primero medio
2.1 Función lineal con representación gráfica y elementos
2.2 Función afín con representación gráfica y elementos
2.3 Resolución de problemas mediante ecuaciones literales
2.4 Composición de funciones y propiedades asociadas
2.5 Dominio y recorrido de funciones que se obtienen al componer otras funciones
3.- Álgebra para segundo medio
3.1 Función exponencial y representación gráfica
3.2 Función logarítmica y representación gráfica
3.3 Función raíz cuadrada y representación gráfica
3.4 Sistemas de ecuaciones lineales con dos incógnitas
3.5 Métodos de resolución de un sistema de ecuaciones lineales con dos incógnitas
3.6 Gráfica de un sistema de ecuaciones
3.7 Expresiones algebraicas fraccionarias
3.8 Operaciones de expresiones algebraicas fraccionarias
Topic 1
Historia del álgebra
Un corto video introductorio para contextualizar el origen del álgebra.
Topic 2
2.- Álgebra para primero medio
El álgebra para primero medio ofrece la oportunidad a los estudiantes de explorar naturalmente contextos multiplicativos de expresiones algebraicas y desarrollar productos notables y factorizaciones de expresiones algebraicas. Prioriza el desarrollo de multiplicaciones algebraicas, la comprensión de los procedimientos y el descubrimiento de reglas y propiedades a través de la formulación y verificación de conjeturas.
Por otra parte, en cuanto a la progresión en el aprendizaje relacionado con las funciones, se introduce el estudio de las funciones lineal y afín. Se propone a los alumnos identificar y representar dichas funciones a través de tablas, gráficos y algebraicamente.
Finalmente, en este nivel se trabaja la composición de funciones como un paso más en el estudio de funciones.
Para el buen entendimiento de este contenido, se necesitan los siguientes conocimientos previos:
› Concepto de variable
› Dependencia e independencia de variables
› Variación proporcional directa e inversa
› Concepto de función
› Dominio y recorrido de una función
› Representación gráfica de funciones
› Ecuación de primer grado con dos incógnitas
2.1 Funciones lineales
Las funciones de proporcionalidad directa o funciones lineales son aquellas cuya gráfica es una línea recta que pasa por el origen de coordenadas; su expresión algebraica es y = mx , siendo m la constante de proporcionalidad.
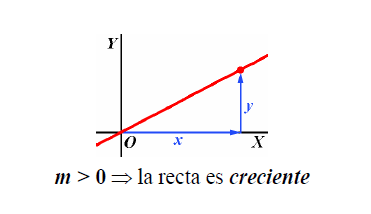
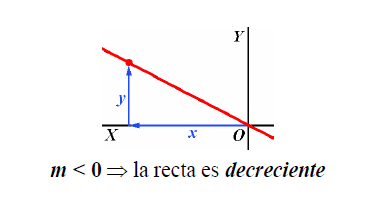
Pendiente
En la función lineal y = mx, al coeficiente m (constante de proporcionalidad) se le llama pendiente de la recta y se halla dividiendo el valor de la variable dependiente por el correspondiente valor de la variable independiente.
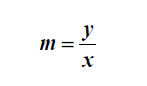
Su valor es la medida del crecimiento o decrecimiento de la recta de ecuación y = mx , y nos indica la variación de la variable y porcada incremento de una unidad de la variable x .
La pendiente de una recta nos proporciona la inclinación de la misma respecto del eje X (ángulo que forma la recta con dicho eje). En el siguiente ejemplo puedes observar que cuanto mayor es la pendiente, mayor es la inclinación de la recta.
2.2 Funciones afín
Las funciones afines son aquellas cuya gráfica es una línea recta que no pasa por el origen de coordenadas; su expresión algebraica es y = mx + n.
En la expresión anterior:
· m es la pendiente de la recta.
· n es la ordenada en el origen: la recta corta al eje de ordenadas en el punto (0, n).
- Gráfica de una función afín
Nótese que una función lineal es una función afín solo que tiene el coeficiente de posición (n) igual a cero.
2.3 Resolución de problemas mediante ecuaciones literales.
Una ecuación literal es aquella en la que una o más de las cantidades conocidas se representan mediante el uso de letras. Por lo general, dichas cantidades conocidas se representan con las primeras letras del alfabeto a, b, c... y las incógnitas con las letras finales x, y, z.
Ejemplo:
a + bx = dy
En este ejemplo las letras a, b, d, son cantidades conocidas, mientras que x e y, representan las incógnitas de la ecuación.
Otro ejemplo de este tipo de ecuaciones, lo podemos encontrar en fórmulas de perímetros, áreas, volúmenes, etc. donde se haga uso de literales.
Para resolver estas ecuaciones se aplican las mismas reglas que se utilizan en la resolución de ecuaciones ordinarias:
Primero, se efectúan las operaciones indicadas, si las hay.
Luego, se trasladan los términos, para agrupar en un miembro los términos que contengan la incógnita y en el otro miembro, los términos que no contienen la incógnita y por lo tanto son conocidos (aunque estén expresados con letras).
En un tercer paso, lo prudente es reducir los términos semejantes en los dos miembros, para que sea más fácil el manejo de la incógnita.
Se despeja la incógnita. Para poder despejar la incógnita, es útil recordar que en una igualdad podemos hacer operaciones iguales a los dos miembros, sin alterar la igualdad.
2.4 Composición de funciones y propiedades asociadas
Función compuesta
Dadas dos funciones f(x) y g(x), se llama función compuesta de f con g, y escribimos g o f, a aquella función en la que la imagen de un número real x es el resultado de actuar sucesivamente sobre x primero f y después g.
Para hallar la expresión analítica de la función compuesta de dos funciones se aplica el resultado anterior:
(gof) (x) = f[g(x)].Ejemplo: Sean las funciones f(x) = 3x - 2 y g(x) = 2x + 5; entonces la función compuesta de f con g es (gof)(x) = g[f(x)] = g(3x - 2) = 2(3x - 2) + 5 = 6x - 4 + 5 = 6x + 1.
En el razonamiento anterior se ha tenido en cuenta que si g(x) = 2x + 5, y por lo tanto,
g(3x - 2) = 2(3x - 2) + 5.Propiedades de la composición
ASOCIATIVA: Dadas tres funciones cualesquiera f(x), g(x) y h(x) se cumple que ho(gof) = (hog)of.
CONMUTATIVA: La composición de funciones en general no es conmutativa, es decir, gof y fog son en general dos funciones distintas.
En el ejemplo anterior (gof)(x) =6x + 1, sin embargo, (fog)(x) = f[g(x)] = f(2x + 5) = 3(2x + 5) - 2 = 6x + 15 - 2 = 6x + 13, luego las funciones gof y fog son distintas.
FUNCIÓN IDENTIDAD: La función i(x) = a que hace corresponder a cada número real con él mismo, al componerla con cualquier función f(x) da de resultado f(x). Además i(x) conmuta con todas las funciones, por tanto i(x) es el elemento neutro de la composición de funciones.
- Funciones compuestas
- 2.5 Dominio y Recorrido de funciones compuestas
Dominio de una función compuesta
- Recorrido de una función
Topic 3
Álgebra para segundo medio
Los alumnos han estudiado en años anteriores el concepto de función y, en particular, la función lineal y afín. En esta unidad se introducen las funciones exponencial, logaritmo y raíz cuadrada en diversos contextos y las respectivas representaciones gráficas con la ayuda de herramientas tecnológicas. Por otra parte, se enseña la resolución de sistemas de ecuaciones lineales con dos incógnitas, estrechamente ligada a la resolución de problemas. Además, se puede apoyar la representación gráfica de estos sistemas con herramientas tecnológicas. Con respecto a las expresiones algebraicas, los estudiantes generalizarán las estrategias que usaban en las operaciones de números fraccionarios para operar con expresiones algebraicas fraccionarias e identificarán los valores para los cuales se indefine una fracción algebraica.
3.1 Funciones exponenciales y representación gráfica
La función exponencial
La función exponencial es de la forma y=ax, siendo "a" un número real positivo.
En la figura se ve el trazado de la gráfica de y=2x.
x
-3
-2
-1
0
1
2
3
-0,5
y
0,125
0,25
0,5
1
2
4
8
-2
En los gráficos inferiores se puede ver como cambia la gráfica al variar a. Observa que las gráficas de y=ax y de y=(1/a)x=a-x son simétricas respecto del eje OY.
En las gráficas de arriba se puede ver como al multiplicar poruna constante y=k·ax el punto de corte con el eje OY es (0,k). Al sumar (o restar) una constante b la gráfica se desplaza hacia arriba (o hacia abajo) b unidades y la asíntota horizontal pasa a ser y=b.
• El dominio son todos los reales y el recorrido son los reales positivos.
• Es continua.
• Si a>1 la función es creciente y si 0<a<1 es decreciente.
• Corta al eje OY en (0,1).
• El eje OX es asíntota.
• La función es inyectiva, esto es si am=an entonces m=n.
Crecimiento exponencial
La función exponencial se presenta en multitud de fenómenos de crecimiento animal, vegetal, económico, etc. En todos ellos la variable es el tiempo.
En el crecimiento exponencial, cada valor de y se obtiene multiplicando el valor anterior por una cantidad constante a.
Donde k es el valor inicial (para t=0), t es el tiempo transcurrido y a es el factor por el que se multiplica en cada unidad de tiempo.
Si 0<a<1 se trata de un decrecimiento exponencial.- Ejemplo:
En un laboratorio tienen un cultivo bacteriano, si su peso se multiplica por 2 cada día, ¿cuál es su crecimiento si el peso inicial es 3 gr?
- 3.2 Funciones logarítmicas y representación gráfica
La función inversa de la exponencial
Dada una función inyectiva, y=f(x), se llama función inversa de f a otra función, g, tal que g(y)=x. En la figura adjunta se puede ver la inversa de la función exponencial.
Para cada x se obtiene ax. Al valor obtenido lo llamamos y o f(x). La función inversa de la exponencial es la que cumple que g(y)=x.
Esta función se llama función logarítmica y, como puedes observar, es simétrica de la función exponencial con respecto a la bisectriz del primer y tercer cuadrantes.
La función logarítmica
Es la función inversa de la función exponencial y se denota de la siguiente manera: y = logax, con a>0 y distinto de 1.
En la figura se representa la gráfica de y=log2x de forma similar a como se hizo con la exponencial. Sus propiedades son "simétricas".
x
0,125
0,25
0,5
1
2
4
8
f(x)
-3
-2
-1
0
1
2
3
En los gráficos inferiores se puede ver como cambia la gráfica al variar a. 
• El dominio son los reales positivos y el recorrido son todos los reales.
• Es continua.
• Si a>1 la función es creciente y si 0<a<1 es decreciente.
• Corta al eje OX en (1,0).
• El eje OY es asíntota.
• La función es inyectiva, esto es si am=an entonces m=n.
En las gráficas de la derecha se puede ver como al multiplicar por una constante y=k·logax cambia la rapidez con que la función crece o decrece (k<0).
Al sumar (o restar) una constante b la gráfica se desplaza hacia arriba (o hacia abajo) b unidades, cambiando el punto de corte con el eje de abscisas.
- 3.3 Función raíz cuadrada y representación gráfica
Función raíz cuadrada
La función raíz cuadrada de un número, es el número mayor o igual que cero, que elevado al cuadrado se obtiene el primer número. Su notación es = ?x
Por ejemplo 9 = ?9 si calculamos el valor ?9 = 3 , puesto que 3^2 = 9.
Es importante aclarar que como condición se mencionó anteriormente que el número obtenido debía ser mayor o igual a cero, por esto no consideramos que ?9 = ?3, siendo que se cumple que (?3)^2= 9.
f(x) = ?xAlgunos ejemplos
f(4)= ?4 = 2
f(25) = ?25 = 5
f(?9) = ??9 no definida en IR , su solución es un número complejo.
Para realizar su gráfica podemos tomar algunos valores
x=0
x=1
x=2
x=3
x=4
x=5
x=6
x=7
x=8
x=9
f(x)
?0 ?1 ?2 ?3 ?4 ?5 ?6 ?7 ?8 ?9
0
1
2
3
Sólo algunos de ellos son valores exactos, que son los que nos ayudarán a trazar su gráfica.
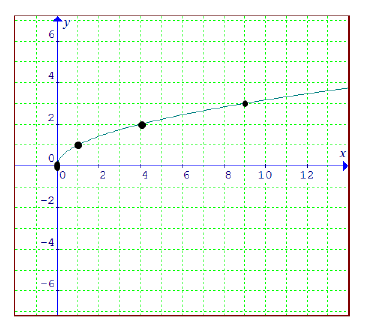
Podemos visualizar que Dom f = [0,?[ y también que Rec f = [0,?[
- 3.4 Sistemas de ecuaciones lineales con dos incognitas
Se llama sistema de ecuaciones lineales a un conjunto de ecuaciones de la forma:
donde x1, ..., xn son las incógnitas, b1, ..., bm se denominan términos independientes y los números aij se llaman coeficientes de las incógnitas, formando una matriz que denominaremos A, matriz de coeficientes. Cuando el término independiente sea cero, estamos ante un caso particular de sistemas que denominamos homogéneos.
Un conjunto de n números que verifiquen todas las ecuaciones se llama solución del sistema. Dado un sistema de ecuaciones, el objetivo principal es hallar todas sus soluciones, es decir, hallar todos los valores de x1, ..., xn que verifican todas las ecuaciones.
Atendiendo al número de soluciones, los sistemas de ecuaciones lineales podemos clasificarlos en tres tipos:
Sistema incompatible: son aquellos que no poseen solución.
Sistema compatible: son aquellos que poseen solución. Dentro de ellos, podemos hablar de:
Sistema compatible determinado: sistemas con una única solución.
Sistema compatible indeterminado: sistemas con infinitas soluciones.
En un sistema de ecuaciones lineales sólo se pueden dar estas tres situaciones, es decir, o no tiene solución, o tiene una, o tiene infinitas, por lo tanto, nunca podemos encontrar un sistema lineal, con, por ejemplo, tres soluciones.
- 3.5 Método de resolución de ecuaciones lineales con dos incognitas
Método de Igualación:
Método de Sustitución:
Método de Reducción:
3.6 Gráfica de un sistema de ecuaciones
A veces, graficar una sola ecuación lineal es todo lo que se necesita para resolver un problema matemático. Otras veces, una sola línea simplemente no nos sirve, y se necesita una segunda ecuación para modelar la situación. Este es normalmente el caso cuando un problema tiene dos variables. Resolver este tipo de problemas requiere trabajar con un sistema de ecuaciones, el cual es un conjunto de dos o más ecuaciones que contienen las mismas incógnitas.
Estudiemos los sistemas de ecuaciones, para ver qué nos revelan las gráficas de ecuaciones individuales sobre la relación matemática entre las variables.
Sistema de ecuaciones
Un sistema de ecuaciones contiene dos o más ecuaciones lineales que comparten dos o más incógnitas. Para encontrar la solución de un sistema de ecuaciones, debemos encontrar un valor (o rango de valores) que satisfagan todas las ecuaciones en el sistema.
Las gráficas de ecuaciones del sistema nos pueden decir cuántas soluciones existen en ese sistema. Ve las imágenes abajo. Cada una muestra dos rectas que conforman un sistema de ecuaciones (en la gráfica de la derecha las dos rectas se enciman y parecen una sola línea). ¿Cuántos puntos en común revelan cada uno de los sistemas?
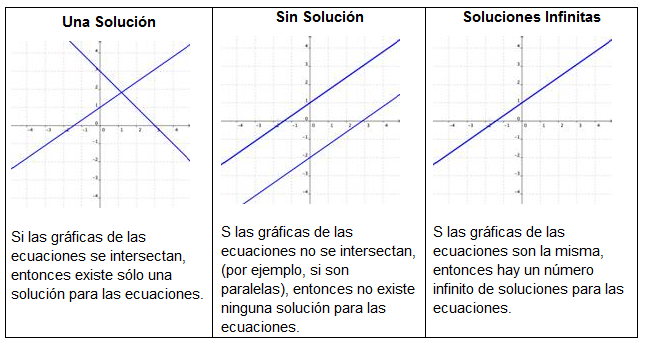Recuerda, la gráfica de una recta representa cada punto que es una posible solución para la ecuación de dicha recta. Por lo que cuando las gráficas de dos ecuaciones se cruzan, el punto de intersección es común en ambas rectas, lo que significa que es una posible solución para ambas ecuaciones. Cuando las gráficas de dos ecuaciones nunca se tocan, no hay puntos comunes y no hay soluciones posibles para el sistema. Cuando las gráficas de dos ecuaciones quedan una encima de la otra, comparten todos sus puntos y cada uno de ellos es una posible solución.
3.7 Expresiones algebraicas fraccionarias
Las expresiones algebraicas fraccionarias o fracciones algebraicas, no son otra cosa que fracciones en las cuales el numerador y el denominador son expresiones algebraicas, es decir polinomios.Una definición formal sería:
Sean P(x) y Q(x) dos polinomios, con Q(x) distinto de cero. Es una fracción algebraica toda expresión de la forma P(x)/Q(x)
Si tu primera reacción al leer esto de fracciones con polinomio fue, ( ¿cómo decirlo en forma diplomática? ) ..., maldecir ... al que “invento” esto, te diré que no eres el único.
Sin embargo a no desesperar, que no es tan difícil.
3.8 Operaciones de expresiones algebraicas fraccionarias
Suma
Resta
Multiplicación
División
Topic 4
Últimas actividades
Recuerde que debe hacer todas las actividades descritas en el curso, ya que cada una aporta con un porcentaje para la nota final.
Más abajo encontrará las últimas actividades que debe realizar, que consisten en:
- Resolver una prueba general de carácter sumativa.
- Responder a una encuesta, que se mide en la participación del alumno.
Los puntajes para obtener la nota final son:
TRABAJOS PRÁCTICOS = 25%
PRUEBAS SUMATIVAS POR CONTENIDO O AUTOEVALUACIONES = 20%
PRUEBA FINAL DEL CURSO = 45%
PARTICIPACIÓN = 10%