¿Qué es un prisma?
Un prisma es un cuerpo geométrico formado por dos caras planas poligonales, paralelas e iguales, que se llaman bases, y tantas caras rectangulares como lados tiene cada base.
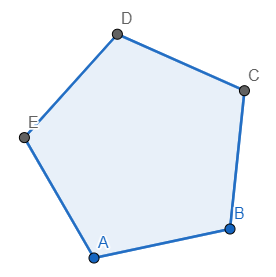
Decimos que un prisma es regular cuando su base es un polígono regular

(en esta imágen se presenta un prisma regular de base pentagonal)
Un prisma puede ser generado por la traslación de un polígono en un plano hacia un espacio mediante un vector de 3 coordenadas. Por tanto un prisma existe en un espacio de 3 dimensiones, al prisma le podemos calcular su área y volumen.
¿Cómo calcular el área de un prisma?
Recordemos que cuando hablábamos de área de figuras geométricas nos referíamos a la superficie de la figura, en el caso de un prisma, dicha superficie está conformada el área de sus 2 caras basales y el área de sus caras laterales, notemos que, la cantidad de caras laterales dependerá de la cantidad de lados que tenga la base. Así, de manera intuitiva, podemos notar que el área de un prisma estará dado por:
\( 2 \cdot Área \; Basal + n \cdot Área \; de \; cara \; lateral \) (con n, la cantidad de caras laterales del prisma)
notemos que en este tipo de prismas, las caras laterales son rectángulos, por lo que para el área lateral, necesitaremos saber la altura del prisma y el largo de los lados de las caras basales. Pero, ¿Cómo podemos calcular el área de las caras basales?
Si la base es un triángulo, entonces sabemos que su área está dada por: \( \dfrac{(base * altura)}{2} \)
Si la base es un cuadrado, entonces:
\( lado \cdot lado = l^2 \)Pero, ¿Cómo se calcula el área de un pentágono?¿Y de un hexágono? etc.
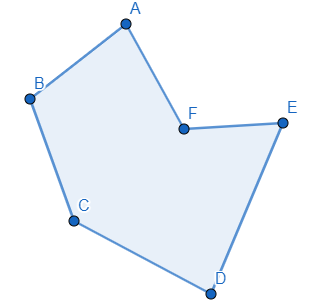
Bien, piensa en un polígono cualquiera
¿Puedes dividirlo de tal forma que calcular su área sea más fácil?
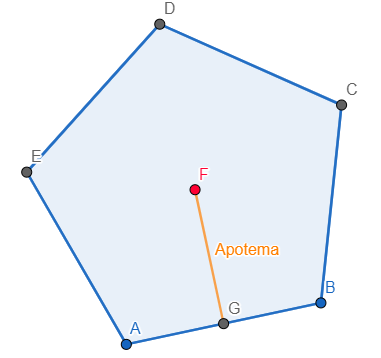
en efecto, podemos dividir cualquier polígono en triángulos para calcular su área por separado (asumiendo que es posible conocer la altura de cada uno de estos). Pero, ¿Cómo funciona esto en un polígono regular? Tomemos por ejemplo el siguiente pentágono:
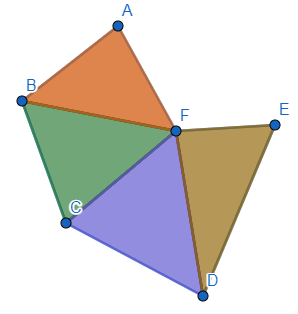
Si aplicamos la idea anterior tendremos algo así:
Sin embargo, tenemos que preguntarnos, ¿es posible conocer las alturas de estos triángulos? Ahora bien, tal vez podamos aprovechar el hecho de que estamos trabajando con un polígono regular para obtener una mejor forma de dividir nuestra figura.
Para ello, debemos saber que al trabajar con un polígono regular, este cuenta con un centro y con una apotema, esta última, es la menor distancia que hay entre el centro y los lados del polígono.
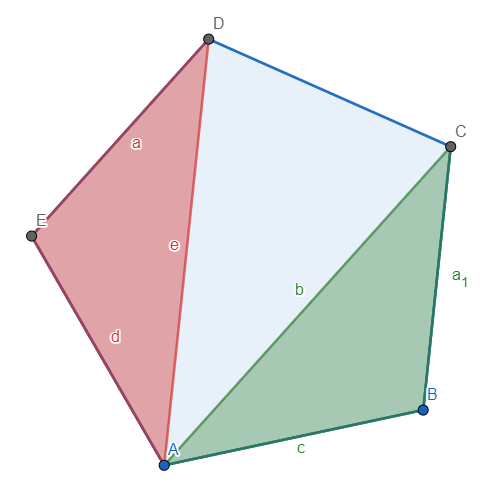
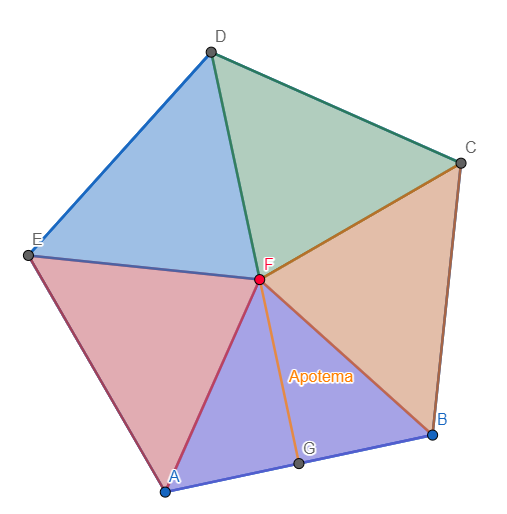
Ahora, notemos que usando el centro del polígono regular, podemos dividirlo en triángulos tal que así:
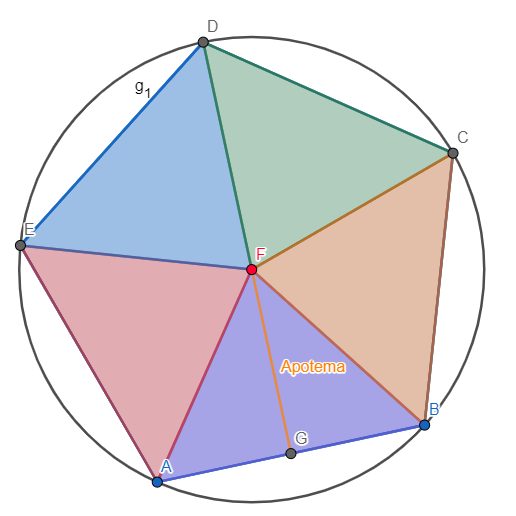
Ahora bien, dado a que un polígono regular se puede inscribir en una circunferencia como sigue:
Podemos observar que la distancia desde el centro F a los vértices del polígono es la misma, pues dicha distancia equivale al
radio de la circunferencia, además, como el lado basal de cada triángulo isósceles (considerando la apotema como altura) corresponde a un lado del polígono regular (y por lo tanto, miden lo mismo), tenemos que los 5 triángulos generados son congruentes y por lo tanto, tienen la misma área. Así, el área basal de un pentágono será igual a: \( 5 \cdot \dfrac{l \cdot a}{2} \) , con l la medida del lado del polígono regular y a la medida de la apotema
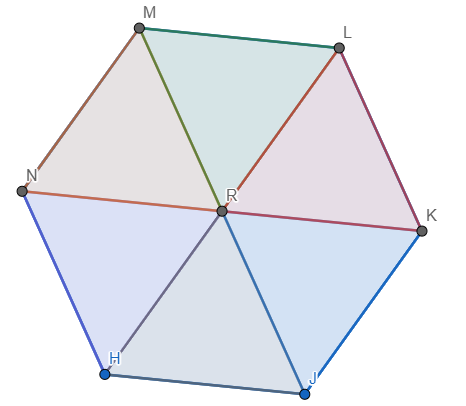
Ahora bien, notemos que para un hexágono regular ocurre lo mismo:
Solo que ahora en lugar de 5 triángulos tenemos 6, para el heptágono serán 7, para el octágono, 8, y así. Para generalizar, tendremos que dado un polígono de n lados, (con \( n \geq 5 \)), entonces, su área estará dada por:
\( n\cdot \dfrac{l \cdot a}{2} \) o bien \( \dfrac{perímetro \cdot apotema}{2} \)
(notemos que en este caso, \( n \cdot l \) equivale al perímetro).
Observación: la fórmula igual es válida para un cuadrado, o un triángulo equilátero, sin embargo para estos casos se recomienda calcular el área como \( l^2 \) o \( \dfrac{base \cdot altura}{2} \) respectivamente
Por lo tanto, notemos que un prisma tiene tantas caras laterales como lados tenga su base, y ya que sus caras laterales corresponden a rectángulos, y el área de un rectángulo se obtiene de multiplicar la base del rectángulo por su altura, el área de un prisma de base regular será determinada por:
\( 2\cdot área_{base} + n \cdot h
\)
con n, la cantidad de lados de la base, y h la altura del prisma
Ejemplos
Calcule el área de los siguientes prismas:
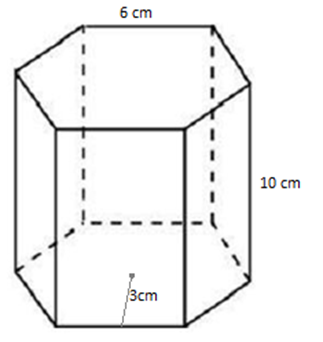
Área: \( 2 \bigg(6\cdot \dfrac{3\cdot6}{2}\bigg)+6\cdot10\cdot6= 108+360= 468\, cm^2 \)
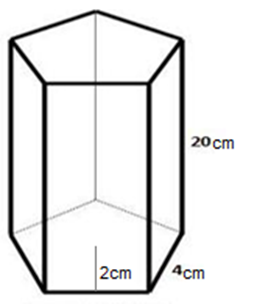
Área: \( 2 \bigg(5\cdot \dfrac{2\cdot4}{2}\bigg)+5\cdot20\cdot4= 40+400= 440\, cm^2 \)