Conos
¿Qué es un cono?
Un cono es un sólido de revolución generado, al rotar un triángulo rectángulo alrededor de uno de sus catetos (aunque también se puede generar rotando un triángulo isósceles utilizando como eje la altura del triángulo isósceles).
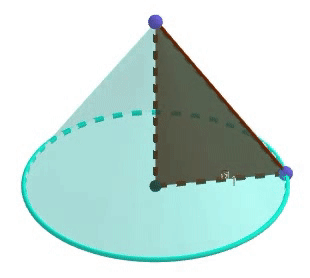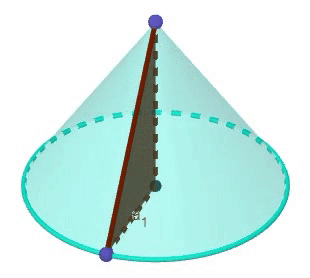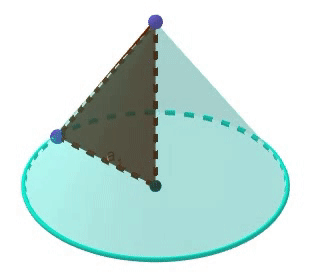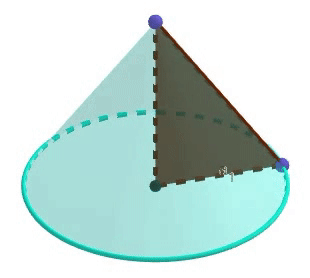
Destacar que al cateto utilizado como eje de rotación determina la altura del cono, mientras que el restante, determinará el radio de la base, además, la hipotenusa de el triángulo rectángulo que se ve en la imágen, se le denomina "generatriz"
Área de un cono
Notemos que podemos "desarmar" un cono en su base (círculo) y en su cara lateral (sección circular)
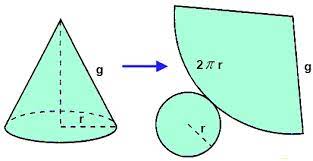
Ahora bien, notemos que la sección circular que forma su cara lateral, posee radio g (medida de la generatriz) y arco 2πr (perímetro de la circunferencia basal) luego, para calcular el área de esta sección circular podemos imaginarnos un círculo de radio g al que pertenezca dicha sección circular.
Notemos que el área de este círculo, sería πg2 y su perímetro 2πg :
| Círculo | Sección circular | |
|---|---|---|
| Área | πg2 | x |
| Perímetro | 2πg | 2πr |
\( \Rightarrow x=\dfrac{\pi g^2 \cdot 2\pi r}{2\pi g}=\pi rg \)
Luego, el área de un cono está dada por:
\( A_{cono}=\pi rg+\pi r^2 \)
donde r es el radio de la base y g la generatriz del cono.
Volúmen de un cono
Para encontrar la fórmula del volumen de un cono, podemos hacer uso del Principio de Cavalieri que nos dice que si 2 figuras tienen la misma altura y la misma área de secciones transversales en cada punto a lo largo de esa altura, tienen el mismo volumen. (para entender mejor esto, se recomienda ver este video de KhanAcademyEspañol).
Respecto a la aplicación de dicho principio para encontrar la fórmula del volumen de un cono, se recomienda ver el siguiente video de Álgebra Para Todos
Fórmula del Volumen de un cono: \( \dfrac{1}{3} Área \; basal \cdot altura = \dfrac{\pi r^2h}{3} \)
Ejemplo:
Calcule el área y volumen del siguiente cono:
Para calcular el área, primero tenemos que calcular la generatriz utilizando el teorema de Pitágoras, sin embargo, notemos que los catetos de este triángulo rectángulo miden 3 y 4 centímetros respectivamente, por lo tanto, la generatriz mide 5 cm (terna pitagórica)
de todas formas, el cálculo sería así:
\( \, \,3^2+4^2=g^2 \\ \sqrt{3^2+4^2}=\sqrt{g^2} \\ \sqrt{9+16}=|g| \\ \sqrt{25}=|g| \Rightarrow g= 5 \, cm \)
Ahora, utilizamos las fórmulas y calculamos:
Área: \( \pi \cdot 3 \cdot 5 + \pi \cdot 3^2 = 15\pi+9\pi = 24\pi \, cm^2 \)
Volumen: \( \dfrac{\pi\cdot3^2\cdot4}{3}=12\pi \, cm^3 \)
Última modificación: sábado, 3 de diciembre de 2022, 21:52