Dominio de una Función

El dominio 

de una función es el conjunto sobre el que se define la función. En una función f : A→B

Esta función se ha definido sobre los números reales, pero, en realidad, la función no está definida en todos los reales. Más exactamente, la función no está definida en 0 porque no se puede calcular su imagen: f (0) =1/0f (0) =1/0.

en si, el dominio son todos los posibles valores que puede tomar X en la función, donde esta no se anula, por esta razón en el ejemplo anterior se dice que puede tomar todos los valores en el conjunto de los números reales, pero no en el 0, puesto que en los números Reales no existe la división por cero.

luego el dominio de la función se puede escribir como:

 El dominio de esta función es todos los reales excepto 0 :  

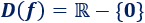
generalmente nos pueden dar el dominio de una función cuando la definen, como es el ejemplo anterior. pero en el caso de que no sea así, y nos pidan calcular el dominio. es cansillo verlo, una forma es ver la grafica de la función. y la otra forma es calcularla "manualmente", esto es: